js中浮点数精度问题

共计 547 字，约需阅读 1.99 分钟

在商品的价格计算中，由于精度的需要，要把用户输入的价格从元转化为分，其转化规则如下

1
2
const price = Number(inputPrice) * 100
console.log(price)

但是在测试过程中发现，输入 2.01 时，输出结果不为 201 ，而是 200.99999999999997
通过研究发现和 js 的数字存储方式 IEEE 754 有关，计算机存储数字时，由于存储方式的原因，存储的并不是准确的数字，而是有一定误差的数字，如经典的

1
2
0.1 + 0.2 === 0.3
false

IEEE 754 浮点数

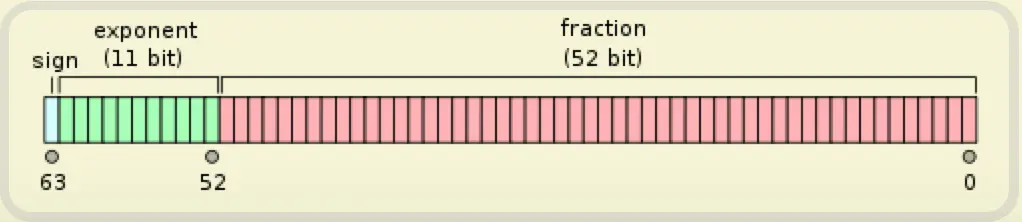
IEEE 754 浮点数表示

IEEE 754 浮点数由三个域组成，分别为 sign bit (符号位)、exponent bias (指数偏移值) 和 fraction (尾数)。64 位中，sign bit 占 1 位，exponent bias 占 11 位，fraction 占 52 位。

0.1 转换为二进制表示

小数转二进制用乘 R 取整的方法，运算如下

小数 x2 的结果 整数部分
0.1 0.2 0
0.2 0.4 0
0.4 0.8 0
0.8 1.6 1
0.6 1.2 1
0.2 0.4 0
0.4 0.8 0
0.8 1.6 1
0.6 1.2 1
0.2 0.4 0
… … …

结果 0.00011001100110011…(循环 0011), 将转换后的二进制通过科学计数法表示 0.00011...(无限重复 0011) 通过科学计数法表示则是 1.10011001...(重复 1001)*2 - 4(偏移 4 位)

指数偏移值

双精度浮点数固定偏移值 (2^(11-1)-1) 加上指数实际值(即 2^-4 中的 -4) 的 11 位二进制表示。

注： exponent bias 在 64 位中占 11 位
尾数

fraction 占 52 位所以抽取 52 位小数（多出来的采用四舍五入制）

结果

1
1001...(中间有 11 个 1001)...1010 (请注意最后四位，是 1010 而不是 1001，因为四舍五入有进位）

处理办法

可以通过四舍五入的方式进行取整，保证数据的准确性

toFixed

具备自动四舍五入的能力

1
2
const price = Number((Number(inputPrice) * 100).toFixed())
console.log(price)

参考